COMPOSING BY NUMBERS – SUMMARY by Dorota Walentynowicz
LECTURE 1 – PYTHAGOREANS
The school: We speak of Pythagoreans rather than of Pythagoras, because little is known of the founder and, therefore it is difficult to assign to any individual the characteristic Pythagorean doctrines. The term „Pythagoreism” refers to the whole of religious, ethic, moral, political and even aesthetic doctrines and concepts formed in VI/V c. BC, assigned by the tradition to Pythagoras himself. Pythagoreism is also a sensu stricto philosophical current formed by the Pythagorean school. And finally we interpret the term „Pythagoreism”, as Plato did, as a certain model of living in a community introduced by the Pythagorean communities, obeying the rules assigned by their master. Pythagorean philosophy came to an end in IV c. BC but Pythagoreism persisted as a form of attitude and model of life until III c. AD.
Mysticism: Pythagoras was believed to be the descendant of Hermes Psychopompos: the Greek god Hermes was responsible for bringing the souls to the underworld and was considered the patron of any secret knowledge (hermetic) – connecting Pythagoras to this particular deity indicates the mystical character of his teaching
Harmony: Aristoteles in “De anima” - „the tradition has passed on still another theory of the soul; they [who are in favor of it] say that the soul is a certain kind of harmony, because harmony is a mixture and synthesis of the adverse things”.
According to Pythagoras the soul was a force, which, taking as an example the harmony of cosmic elements, keeps a similar harmony in the human being. The man is supposed to imitate the order (Greek “cosmos” means „order”) of the universe, thus deserving to be called a microcosm.
Numerical order: Having discovered mathematical ratios in all the phenomena of the world, Pythagoreans begun to worship the number, seeing in it the cause and reason of all order and the ruling power of the universe.
„you shall see the nature of the number and its ruling power not only in the daemonic and devine things, but also always and in all of the doings and words of humans” says Philolaos.
Some of the numbers and geometric values were even identified with certain gods or devoted to the highest deities of Greek pantheon.
Philolaos, a contemporary of Socrates, uses the numbers to define not only the mind but also all other properties and abilities of a man.
„He defined the physiological functions of the body by number 5, animation by number 6, mind, health and light by number 7. Further he claims that love, friendship, wisdom and perception are in number 8.”
Plato's Timeaus and the Regular Polyhedra: Plato's creator god, the Demiurge, gave the basic elements definite geometrical shapes, but just as small and imperceptible as the atoms. The Demiurge chose the first four regular polyhedra for this purpose, because they were the most perfect, the most beautiful, and therefore the best. As earth is most stable and immobile of elements, God chose the cube, with its large base areas, to constitute it. Fire is the least stable and most mobile, so it is made up of regular triangular pyramids (tetrahedra). Water is more stable than air, so it is composed of regular icosahedra. Plato observes (59d) that the bases of icosahedra "give way" more easily than cubes, so that explains why water is able to flow. Perfect octahedra are left to make up the air. Fire, being composed of the smallest solid with the sharpest points and edges, is the most destructive of the elements.
LECTURE 2 – FROM PYTHAGORAS TO J.S.BACH
Consonance:
According to legend, Pythagoras discovered the foundations of music by listening to the sounds of four blacksmith's hammers, which produced consonance and dissonance when they were struck simultaneously. He found out that the explanation was in the weight ratios. He recognized that consonant musical sounds can relate to simple number ratios.
Perfect consonances: unison 1:1, an octave 1:2, a twelfth 3:1, a double octave 4:1, a fifth 3:2, a fourth 4:3.
Pythagorean coma: 12 perfect fifths (the circle of fifths) do not equal any even octave. What is left is called the Pythagorean coma. The resolution of the Pythagorean coma was the major concern for further development of temperament system.
Until 14th century Pythagorean tuning remained popular, because the perfect fifths and perfect fourths were intervals favored by the early medieval ear (example: ” La Messe de Notre Dame” by G. de Machant). Later composers have exploited a rearrangement of the Pythagorean tuning in order to explore possibilities of more blending thirds and sixths.
Temperament: involves small and deliberate deviations from the ideal interval ratios in order to eliminate the Pythagorean coma and allow transpositions
Pythagorean tuning: pure 5ths and 4ths, active 3rds
Meantone temperament: pure 3rds (standard for 16th and 17th century keyboard instruments)
Well-tempered system: tempers all fifths by different amount thus producing a variety of colors, but still permitting all intervals to be playable at any transposition (18th century)
Equal temperament: equally tempers each fifth to disperse the come
Musurgia universalis by Athanasius Kirchner (1650) was one of the most important musical texts of 17th century and a testament to the world’s understanding in his days. Kirchner, combining Pythagoreism with Catholic orthodoxy, held the essentially medieval view that the cosmos was revealed in musical rations and that musical harmony mirrored God’s harmony. Kirchner – also known as inventor of Cat Organ – introduced rhetorical steps of inventio, dispositio and elocutio into musical theory. The “musica poetica”, as it was called, aimed to reveal the meaning of the text in and through the music.
“Music is a hidden arithmetical exercise which counts off subconsciously in the soul” (Leibnitz)
the Christian numerology:
1 – God (unison)
2 – Son (octave)
3 – holy spirit (fifth)
4 – angelic (fourth)
5- human
7- mysterious, holy
J.S. Bach’s use of mathematics: J.S.Bach was reported to be a member of Societat der Musicalischen Wissenschaft, a society devoted to studying Pythagorean philosophy. He was well-known for his use of various self-referential number games within his works.
The use of numbers in Bach’s works:
- Enumeration (simply counting notes, measures, bars, parts, movements etc.)
- Operation (transformations of the numbers – subtractions, additions etc.)
- Translation (use of gemaria, eg. A=1, B=2, C=3 etc.)
- Interpretation (the meaning and symbolism of numbers, usually religious)
Bach’s favorite numbers:
7. stands for perfection, Creator and Creation, or the Beginning and End
12 used for the Church, the disciples, the congregation
14. the sum of the letters in his name: b+a+c+h = 2+1+3+8=14
his last piece, called “the art of fugue” remained unfinished, as – according to his son’s report – the composer dies where the notes B-A-C-H appear in the counterpoint
example:
Symbolum Nicenum of the B-minor Mass:,"Credo in unum Deum" and "Patrem omnipotentem”:
The total number of measures/bars for these two movements: 129
Apply gematria: C(3)+R(7)+E(5)+D(4)+O(14) = 43.
The number 129 comes from (43 + 43 + 43) x 3. 3 = Triune God
. The word 'Credo' is sung 7 x 7 = 49 times
. The phrase 'in unum Deum' is sung 7 x 12 = 84 times.
At the end of the fugue in "Patrem omnipotentem" Bach inserts in his own hand the total number of measures/bars: 84 = (permutation: C=3 x A=1 x (B=2, H=8) the letters BACH rearranged, but this is permissible, as well as combining the B and H into one number as he did here) 12 x 7 = 84 a combination of time and eternity.
Geometry of counterpoint:
To us today seems obvious that high-pitched notes are high, and low-pitched are low. So it comes as a shock to learn that in ancient Greece high-pitched notes weren't heard as high; in fact the highest pitched note of the classical Greek octave was called nete, the nether, or lowest note. it got this name from the fact that the stringed instrument named a kithara was held with the highest pitched string nearest the ground - just how one holds a guitar today. J. Desprez in “huc me sydereo”- sending Jezus down from Mount Olympus in a descending scale of twelve notes puts the seal on the development of the pitch/height relation. Three centuries later J.S. Bach used that notion of direction as basis for various geometric operations on his musical scores.
- imitation
- melodic inversion
- retrograde
- retrograde inversion
- augmentation
- diminuition
LECTURE 3 – XX CENTURY MUSIC
Towards atonality:
Tonal music is that in which a definite sense of key prevails, in which all the notes are related to a central key note (a tonic): changes of key center can be brought up by modulation
J.Cage: “the octave has no more reason to be divided into 5/6/7/9 equal intervals than to be devided into 36/59 parts. It’s just a matter of establishing limits”
C.Debussy was the first to use a scale different from traditional scale: the whole tone scale, obtained by dividing the octave into 6 equal parts. Other possible divisions of the octave include 31 tone scale (M. Marsenne designed a 31 tone keyboard) and 53 tone scale (confirmed musical system in China in early 18th century)
Serialism: method of composing with 12 tones (dodecaphony). Series – twelve notes of chromatic scale arranged in any order by composer’s choice, as long as each note appears only once. A series forms a tone-row which undergoes transpositions (12 possibilities) and transformations (prime, inversion, retrograde, retrograde-inversion), which combined give 48 different possible forms of the same series (= a set complex).
Integers 0 to 11 can be substituted for pitch-class names by assigning these integers to successive notes of ascending semi-tonal scale, whose initial element, pitch-class 0, will be the same as the first note of a given prime form of the set.
A.Schonberg was the first one to use the method of composing with 12 tones related only to each other, thus negating the tonal system and “emancipating the dissonance”
(1907 – Schonberg abandoned the key signature)
Aleatoric music: music in which some element of the composition is left to chance or some primary element of a composed work’s realization is left to the determination of the performer (alea = dice). P.Bulez spread the definition using it to describe works that give the performer certain liberties with regard to the sequencing and repetition of the parts.
Aleatoric music originates from musical dice games popular in 18th century (Musicalische Wurfelspiele) – one such is attributed to W.A.Mozart: these games consisted of a sequence of musical measures with variations, which were selected by tossing dice.
M.Duchamp – “Musical erratum” (1913) : score for three voices
Duchamp wrote this piece of music by placing notes on the staff in the order in which they were randomly drawn from a bag (25 notes from F below middle C to high F); the text was a “ready-made” picked from a dictionary ( J.Cage: “One way to study music - study Duchamp”)
Indetermined music : J.Cage and I-Ching
“As a composer I should give up making choices and devote myself to asking questions; chance determined answers will open my mind to the world around at the same time changing my music” (J.Cage)
For cage time is the most fundamental music category, it exists prior to both pitch and harmony and can contain musical sounds as well as noise and silence.
“Imaginary landscape 4” – written for 12 radio receivers: each radio was played by two players, one controlled the frequency, the other the volume; Cage wrote precise scripts of timing but could not control what will be transmitted at the moment of the performance – Cage sets up an architecture but then allows the internal décor to be subject to chance operation.
“Music of changes” – in this composition Cage uses I-Ching, Book of Changes, the ancient Chinese oracular. I-Ching is organized according to 64 hexagrams, each consisting of 6 lines. The oracle is consulted by tossing 3 coins. Cage used a computer program which generated I-Ching hexagrams as if by throwing coins and later translated the chosen hexagrams into a selection of specific number of alternatives
LECTURE 4 – GAMES AND OTHER STRATEGIES
Many composers of XX century music found numbers and various computational models a useful source of compositional material
- set theory
- game theory
- magic squares
- Fibonacci numbers
- Probabilities
- Physical laws
Ordering structure: how to produce scales on more general level? Mathematic strategies, such as sieves, sets, and probability, can be applied to any characteristic of the sound, provided that it can be ordered. If we take any three values of a given sound characteristic and if we can classify them in such way that one falls in between the two others, then we have an “ordering structure”.
Fibonacci sequence:
I.Xenakis - “Metastasis” pitches based on 12-note rows were assigned a series of durations based on the Fibonacci sequence, along with a range of timbres
K.Stockhausen – “Klaverstuck IX”: a mathematical structure undergirds the gradual dissolution of the piece; the grouping of subsections and choice of tempi are partly dictated by the Fibonacci series [1, 2, 3, 5, 8, 13, 21, 34, 55, . . .]
C.Debussy – “Image, reflection in Water”: the Fibonacci numbers are apparent in the organization of sections; sequence of keys is marked out by the intervals 34, 21, 13, and 8
B.Bartok – “Music for string, percussion and celeste” : the xylophon progression appears in intervals 1:2:3:5:8:5:3:2:1
Probability theory - Stochastic music :
Probability concepts are applied across mathematics when considering random structures. What is probability? – when something repeats itself, but not exactly. When we toss a coin we know that the result will be either heads or tails. When we toss it ten times we can’t say forehead how often it will land on one side or the other. When we repeat this many times then the proportion of heads and tails approaches the value of ½. It is therefore a matter of convergence, meeting the target point. That point is “stochos” (Greek for target : the word “stochastic” was used in17th century in a connection with probability theory).
I.Xenakis “ST” – 9 works composed exploring the stochastic method in order to systematize random events
Sieve/ set theory:
I.Xenakis uses the sieve theory to compose his scales. Sieve theory is a set of general techniques designed to estimate the size of sifted sets of integers. Sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to a specified integer.
Physical laws: control of mass events and recognition of laws that govern nature
(eg. I. Xenakis “Metastasis” changes intensity, register, and density of scoring as the musical analogues of mass and energy)
- kinetic gas theory – particles behaving like billiard balls that will hit each other according to the Newtonian laws of mechanic
- Brown movements – how does a single particle move in a mass of others?
- Markov property – the next move depends only on the current position, and not on the previous state
Graphic structures:
In the works of I. Xenakis, such as “Evryali”, “Mists”, the graphic method of arborescence is used (arbor = tree). The starting point is a graphic structure, drawn on a plane, which undergoes a series of geometric transformations (turn, twist, zoom), based on which the sonic picture is created. CEMAM – graphic electromagnetic system with which you can draw any shape and obtain the corresponding music with the help of computer.
M.Kagel - visually manipulates the forms of traditional notation as a means of developing new music. He creates new musical structures by conceptualizing the visual representation of music. These representations are a combination of classical notation form and geometry. Kagel uses angular relationships to develop new variations utilizing harmonic proportions.
Game theory
Game theory is a branch of applied mathematics that studies decisions that are made in environments where various players interact. It studies the situations where players choose different actions in attempt to maximalize their returns.
(origin of game theory - the so called “marriage contract problem” discussed in the Talmud)
types of games:
- symmetric games: identities of the players can be changed without changing the pay-offs
- zero-sum games: a player benefits only at the cost of the other (one wins exactly as much as the other one looses)
- non-zero-sum games: a gain of one player does not necessary correspond with the loss of the other
- simultaneous games: both players move at the same time, or one is not aware of the choice of the other one when making his
- sequential games: later players have some knowledge about the earlier actions
- games with randomly distributed pay-offs
examples of games:
- prisoner’s dilemma
- chicken
- ultimatum game
- dictator game
- battle of sexes
- deadlock
- matching pennies
- stag hunt
I. Xenakis “Duel”, “Strategy”:
“the game is based on musical events, the tactics, which occur simultaneously, the participants employ a strategy determined by me , which leads to the simultaneity of two particular musical sections out of a number of possibilities. The winner is the one who is more adroit in employing a series of tactics designed to achieve higher final results in accordance with the Matrix of the Game. The winner is the one, who has accumulated the grater number of scores according to the matrix”. (I..Xenakis)
Wolfram tones:
WolframTones is an experiment in applying Wolfram's discoveries to the creation of music. WolframTones works by taking simple programs from Wolfram's computational universe, and using music theory and “Mathematica” algorithms to render them as music. Each program in effect defines a virtual world, with its own special story--and WolframTones captures it as a musical composition. (http://tones.wolfram.com)
synesthetics-in-motion
Tuesday, September 19, 2006
Thursday, September 14, 2006
FIBBONACCI AND THE GOLDEN SECTION
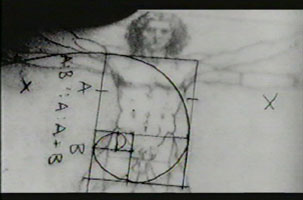
The golden ratio, usually denoted , expresses the relationship that the sum of two quantities is to the larger quantity as the larger is to the smaller. The golden ratio is the following irrational number and numerical approximation:

The figure of a golden section on the right illustrates the defining geometric relationship. Expressed algebraically:



Mario Merz
Tavola a Spirale, 1982
aluminum, glass, fruit, vegetables, branches and beeswax
216 inches diameter
548.6 cm diamete
Pi (Released in 1998)


The golden ratio, usually denoted , expresses the relationship that the sum of two quantities is to the larger quantity as the larger is to the smaller. The golden ratio is the following irrational number and numerical approximation:

The figure of a golden section on the right illustrates the defining geometric relationship. Expressed algebraically:



Mario Merz
Tavola a Spirale, 1982
aluminum, glass, fruit, vegetables, branches and beeswax
216 inches diameter
548.6 cm diamete
Pi (Released in 1998)

THE INTERVAL : PYTHAGORAS AND THEORETICAL MUSIC
(from Nicomachus)
While describing Pythagoras's wisdom in instructing his disciples, we must not fail to note that he invented the harmonic science and ratios. But to explain this we must go a little backwards in time.

Once as he was intently considering music, and reasoning with himself whether it would be possible to devise some instrumental assistance to the sense of hearing, so as to systematize it, as sight is made precise by the compass rule, and [telescope], or touch is made reckonable by balance and measures, - so thinking of these things Pythagoras happened to pass by a brazier's shop, where providentially he heard the hammers beating out a piece of iron on the anvil, producing sounds that harmonized, except one. But he recognized in these sounds, the concord of the octave, the fifth, and the fourth. He saw that the sound between the fourth and the fifth, taken by itself, was a dissonance, and yet completed the greater sound among them. Delighted, therefore, to find that the thing he was anxious to discover had by divine assistance succeeded, he went into the smithy, and by various experiments discovered that the difference of sound arose from the magnitude of the hammers, but not from the force of the strokes, nor from the shape of the hammers, nor from the change of position of the beaten iron. Having then accurately examined the weights and the swing of the hammers, he returned home, and fixed one stake diagonally to the walls, lest some difference should arise from there being several of them, or from some difference in the material of the stakes. From this stake he then suspended four gut-strings, of similar materials, size, thickness and twist. A weight was suspended from the bottom of each. When the strings were equal in length, he struck two of them simultaneously, he reproduced the former intervals, forming different pairs.
He discovered that the string stretched by the greatest weight, when compared with that stretched by the smallest weight, the interval of an octave. The weight of the first was twelve pounds, and that of the latter six. Being therefore in a double ratio, it formed the octave, which was made plain by the weights themselves. Then he found that the string from which the greater weight was suspended compared with that from which was suspended the weight next to the smallest, and which weight was eight pounds, produced the interval known as the fifth. Hence he discovered that this interval is in a ratio of one and a half to one, or three to two, in which ratio the weights also were to each other. The he found that the string stretched by the greatest weight produced, when compared with that which was next to it, in weight, namely, nine pounds, the interval called the fourth, analogous to the weights. This ratio, therefore, he discovered to be in the ratio of one and a third to one, or four to three; while that of the from string from which a weight of nine pounds was suspended to the string which had the smallest weight, again in a ratio of three to two, which is 9 to 6. In like manner, the string next to that from which the small weight was suspended, was to that which had the smallest weight, in the ratio of 4 to 3 (being 8 to 6) but to the string which had the greatest weight, in a ratio of 3 to 2, being 12 to 8. Hence that which is between the fifth and fourth, and by which the fifth exceeds the fourth is proved to be as nine is to eight. But either way it may be proved that the octave is a system consisting of the fifth in conjunction with fourth, just as the double ratio consists of three to two, and four to three; as for instance 12, 8 and 6; or, conversely of the fourth and the fifth, as in the double ratio of four to three and three to two, as for instance, 12, 9 and 6 therefore, and in this order, having confirmed both his hand and hearing to the suspended weights, and having established according to them the ratio of the proportions, by an easy artifice he transferred the common suspension of the strings from the diagonal stake to the head of the instrument which he called "chordotenon," or string-stretcher. Then by the aid of pegs he produced a tension of the strings analogous to that effected by the weights. Employing this method, therefore, as a basis, and as it were an infallible rule, he afterward extended the experiment to other instruments, namely, the striking of pans, to pipes and [r----], to monochords, triangles, and the like in all of which he found the same ratio of numbers to obtain. Then he named the sound which participates in the number 6, tonic; that which participates of the number 8, and is four to three, sub-dominant; that which participates of the number 9, and is one tone higher then the sub-dominant, he called, dominant, and 9 to 8; but that which participates of the number 12, octave.
Then he filled up the middle spaces with analogous sounds in diatonic order, and formed an octochord from symmetric numbers; from the double, the three to two, the four to three, and from the difference of these, the 8 to 9. Thus he discovered the harmonic progression, which tends by a certain physical necessity from the lowest to the most acute sound, diatonically. Later, from the diatonic he progressed to the chromatic and enharmonic orders, as we shall later show when we treat of music. This diatonic scale however, seems to have the following progression, a semi-tone, a tone, and a tone; and this is the fourth, being a system consisting of two tones, and of what is called a semi-tone. Afterwards, adding another tone, we produce the fifth, which is a system consisting of three tones and a semi-tone. Next to this is the system of a semi-tone, a tone, and a tone, forming another fourth, that is, another four to three ratio. Thus in the more ancient octave indeed, all the sounds from the lowest pitch which are with respect to each other fourths, produce everywhere with each other fourths; the semi-tone, by transition, receiving the first, middle and third place, according to that tetrachord. Now in the Pythagoric octave, however, which by conjunction is a system of the tetrachord and pentachord, but if disjoined is a system of two tetrachords separated from each other, the progression is from the gravest to the most acute sound. Hence all sounds that by their distance from each other are fifths, with each other produce the interval of the fifth; the semi-tone successively proceeding into four places, the first, second, third, and fourth.
This is the way in which music is said to have been discovered by Pythagoras. Having reduced it to a system, he delivered it to his disciples to utilize it to produce things as beautiful as possible.
(Iamblichus - This story of the smithy is an ancient error, as pieces of iron give the same note whether struck by heavy or light hammers. Pythagoras may therefore have brought the discovery with him from Egypt, though he may also have developed the further details mentioned in this chapter.)
(from Nicomachus)
While describing Pythagoras's wisdom in instructing his disciples, we must not fail to note that he invented the harmonic science and ratios. But to explain this we must go a little backwards in time.

Once as he was intently considering music, and reasoning with himself whether it would be possible to devise some instrumental assistance to the sense of hearing, so as to systematize it, as sight is made precise by the compass rule, and [telescope], or touch is made reckonable by balance and measures, - so thinking of these things Pythagoras happened to pass by a brazier's shop, where providentially he heard the hammers beating out a piece of iron on the anvil, producing sounds that harmonized, except one. But he recognized in these sounds, the concord of the octave, the fifth, and the fourth. He saw that the sound between the fourth and the fifth, taken by itself, was a dissonance, and yet completed the greater sound among them. Delighted, therefore, to find that the thing he was anxious to discover had by divine assistance succeeded, he went into the smithy, and by various experiments discovered that the difference of sound arose from the magnitude of the hammers, but not from the force of the strokes, nor from the shape of the hammers, nor from the change of position of the beaten iron. Having then accurately examined the weights and the swing of the hammers, he returned home, and fixed one stake diagonally to the walls, lest some difference should arise from there being several of them, or from some difference in the material of the stakes. From this stake he then suspended four gut-strings, of similar materials, size, thickness and twist. A weight was suspended from the bottom of each. When the strings were equal in length, he struck two of them simultaneously, he reproduced the former intervals, forming different pairs.

He discovered that the string stretched by the greatest weight, when compared with that stretched by the smallest weight, the interval of an octave. The weight of the first was twelve pounds, and that of the latter six. Being therefore in a double ratio, it formed the octave, which was made plain by the weights themselves. Then he found that the string from which the greater weight was suspended compared with that from which was suspended the weight next to the smallest, and which weight was eight pounds, produced the interval known as the fifth. Hence he discovered that this interval is in a ratio of one and a half to one, or three to two, in which ratio the weights also were to each other. The he found that the string stretched by the greatest weight produced, when compared with that which was next to it, in weight, namely, nine pounds, the interval called the fourth, analogous to the weights. This ratio, therefore, he discovered to be in the ratio of one and a third to one, or four to three; while that of the from string from which a weight of nine pounds was suspended to the string which had the smallest weight, again in a ratio of three to two, which is 9 to 6. In like manner, the string next to that from which the small weight was suspended, was to that which had the smallest weight, in the ratio of 4 to 3 (being 8 to 6) but to the string which had the greatest weight, in a ratio of 3 to 2, being 12 to 8. Hence that which is between the fifth and fourth, and by which the fifth exceeds the fourth is proved to be as nine is to eight. But either way it may be proved that the octave is a system consisting of the fifth in conjunction with fourth, just as the double ratio consists of three to two, and four to three; as for instance 12, 8 and 6; or, conversely of the fourth and the fifth, as in the double ratio of four to three and three to two, as for instance, 12, 9 and 6 therefore, and in this order, having confirmed both his hand and hearing to the suspended weights, and having established according to them the ratio of the proportions, by an easy artifice he transferred the common suspension of the strings from the diagonal stake to the head of the instrument which he called "chordotenon," or string-stretcher. Then by the aid of pegs he produced a tension of the strings analogous to that effected by the weights. Employing this method, therefore, as a basis, and as it were an infallible rule, he afterward extended the experiment to other instruments, namely, the striking of pans, to pipes and [r----], to monochords, triangles, and the like in all of which he found the same ratio of numbers to obtain. Then he named the sound which participates in the number 6, tonic; that which participates of the number 8, and is four to three, sub-dominant; that which participates of the number 9, and is one tone higher then the sub-dominant, he called, dominant, and 9 to 8; but that which participates of the number 12, octave.
Then he filled up the middle spaces with analogous sounds in diatonic order, and formed an octochord from symmetric numbers; from the double, the three to two, the four to three, and from the difference of these, the 8 to 9. Thus he discovered the harmonic progression, which tends by a certain physical necessity from the lowest to the most acute sound, diatonically. Later, from the diatonic he progressed to the chromatic and enharmonic orders, as we shall later show when we treat of music. This diatonic scale however, seems to have the following progression, a semi-tone, a tone, and a tone; and this is the fourth, being a system consisting of two tones, and of what is called a semi-tone. Afterwards, adding another tone, we produce the fifth, which is a system consisting of three tones and a semi-tone. Next to this is the system of a semi-tone, a tone, and a tone, forming another fourth, that is, another four to three ratio. Thus in the more ancient octave indeed, all the sounds from the lowest pitch which are with respect to each other fourths, produce everywhere with each other fourths; the semi-tone, by transition, receiving the first, middle and third place, according to that tetrachord. Now in the Pythagoric octave, however, which by conjunction is a system of the tetrachord and pentachord, but if disjoined is a system of two tetrachords separated from each other, the progression is from the gravest to the most acute sound. Hence all sounds that by their distance from each other are fifths, with each other produce the interval of the fifth; the semi-tone successively proceeding into four places, the first, second, third, and fourth.
This is the way in which music is said to have been discovered by Pythagoras. Having reduced it to a system, he delivered it to his disciples to utilize it to produce things as beautiful as possible.
(Iamblichus - This story of the smithy is an ancient error, as pieces of iron give the same note whether struck by heavy or light hammers. Pythagoras may therefore have brought the discovery with him from Egypt, though he may also have developed the further details mentioned in this chapter.)
Wednesday, September 13, 2006
PURE LOGIC - GEOMETRY AS A DEDUCTIVE SYSTEM
There is a legend that Pythagoras wanted to see if he could teach someone geometry. after finding a somewhat reluctant student, Pythagoras agreed to pay him a penny for each theorem he learned. because the student was very poor he worked diligently. After a time, however, the student realized that he had become more interested in geometry thatn in the money he was accumulating. in fact, he became so intrigued with his studies that he begged Pythagoras to go faster, offering now to pay him back a penny for each new theorem. Eventually Pythagoras got all of his money back.
What is there about geometry that student could have found so fascinating? Perhaps it was the logical way in which Pythagoras was able to present it. geometry was the first system of ideas developed by man in which a few simple statements were assumed and then used to derive more complex ones. Sucha a system is called deductive.
One of the goals of studying geometry is to develop the ability to think critically. An understanding of the methods of deductive reasoning is fundamental in the development of critical thinking, and therefore we should devote some attention to this subject:
drawing conclusions/ conditional statements/ equivalent statements/ valid and invalid deductions/ undefined terms and definitions/ direct and indirect proofs/ arguments with several premises
Lewis Carroll, the author of Alice's Adventures in Wonderland, and Through the Looking Glass, was a mathematics teacher who write stories as a hobby. His books contain many amusing examples of both good and deliberately poor logic and, as a result, have long been favorites among mathematicians.

Consider the following conversation held at the Mad Hatter's tea party:
"Then you should say what you mean", the March Hare went on,
"I do", Alice hastily replied; "at least - at least I mean what I say - that's the same thing, you know."
"Not the same thing a bit!" said the Hatter. "Why, you might just as well say that 'I see what I eat' is the same thing as 'I eat what I see'!"
"You might just as well say," added the March Hare, "that 'I like what I get' is the same as 'I get what I like'!"
"You might just as well say," added the Dormouse, who seemed to be talking in his sleep, "that 'I breathe when I sleep' is the same thing as 'I sleep when I breathe'!"
"it is the same thing with you," said the Hutter, and here the conversation dropped, adn the party sat silent for a minute.
There is a legend that Pythagoras wanted to see if he could teach someone geometry. after finding a somewhat reluctant student, Pythagoras agreed to pay him a penny for each theorem he learned. because the student was very poor he worked diligently. After a time, however, the student realized that he had become more interested in geometry thatn in the money he was accumulating. in fact, he became so intrigued with his studies that he begged Pythagoras to go faster, offering now to pay him back a penny for each new theorem. Eventually Pythagoras got all of his money back.
What is there about geometry that student could have found so fascinating? Perhaps it was the logical way in which Pythagoras was able to present it. geometry was the first system of ideas developed by man in which a few simple statements were assumed and then used to derive more complex ones. Sucha a system is called deductive.
One of the goals of studying geometry is to develop the ability to think critically. An understanding of the methods of deductive reasoning is fundamental in the development of critical thinking, and therefore we should devote some attention to this subject:
drawing conclusions/ conditional statements/ equivalent statements/ valid and invalid deductions/ undefined terms and definitions/ direct and indirect proofs/ arguments with several premises
Lewis Carroll, the author of Alice's Adventures in Wonderland, and Through the Looking Glass, was a mathematics teacher who write stories as a hobby. His books contain many amusing examples of both good and deliberately poor logic and, as a result, have long been favorites among mathematicians.

Consider the following conversation held at the Mad Hatter's tea party:
"Then you should say what you mean", the March Hare went on,
"I do", Alice hastily replied; "at least - at least I mean what I say - that's the same thing, you know."
"Not the same thing a bit!" said the Hatter. "Why, you might just as well say that 'I see what I eat' is the same thing as 'I eat what I see'!"
"You might just as well say," added the March Hare, "that 'I like what I get' is the same as 'I get what I like'!"
"You might just as well say," added the Dormouse, who seemed to be talking in his sleep, "that 'I breathe when I sleep' is the same thing as 'I sleep when I breathe'!"
"it is the same thing with you," said the Hutter, and here the conversation dropped, adn the party sat silent for a minute.
MOTION - ZENO'S PARADOXES
(Paradox from the Greek "para doxa" something contrary to opinion)

The third is … that the flying arrow is at rest, which result follows from
the assumption that time is composed of moments … . he says that if
everything when it occupies an equal space is at rest, and if that which
is in locomotion is always in a now, the flying arrow is therefore
motionless. (Aristotle Physics, 239b.30)
Zeno abolishes motion, saying "What is in motion moves neither in the
place it is nor in one in which it is not". (Diogenes Laertius Lives of
Famous Philosophers, ix.72)
This argument against motion explicitly turns on a particular kind of
assumption of plurality: that time is composed of moments (or ‘nows’) and
nothing else. Consider an arrow, apparently in motion, at any instant.
First, Zeno assumes that it travels no distance during that moment -- ‘it
occupies an equal space’ for the whole instant. But the entire period of
its motion contains only instants, all of which contain an arrow at rest,
and so, Zeno concludes, the arrow cannot be moving.

Edweard Muybridge - "Freeze frame", pioneer in stop motion photography

Nude descending a staircase, Marcel Duchamp 1912, a scandal when first shown in the Armory show. The object at each moment is at a fixed position (according to Zeno at rest) how can it then move?
The Paradoxa of Zeno of Elea are an example of ancient Greek abstract reasoning that is even in contradiction to observation. How can it be true that nothing moves when our observation “confirms” Heraclitus statement “everything moves and changes”?
(Paradox from the Greek "para doxa" something contrary to opinion)

The third is … that the flying arrow is at rest, which result follows from
the assumption that time is composed of moments … . he says that if
everything when it occupies an equal space is at rest, and if that which
is in locomotion is always in a now, the flying arrow is therefore
motionless. (Aristotle Physics, 239b.30)
Zeno abolishes motion, saying "What is in motion moves neither in the
place it is nor in one in which it is not". (Diogenes Laertius Lives of
Famous Philosophers, ix.72)
This argument against motion explicitly turns on a particular kind of
assumption of plurality: that time is composed of moments (or ‘nows’) and
nothing else. Consider an arrow, apparently in motion, at any instant.
First, Zeno assumes that it travels no distance during that moment -- ‘it
occupies an equal space’ for the whole instant. But the entire period of
its motion contains only instants, all of which contain an arrow at rest,
and so, Zeno concludes, the arrow cannot be moving.

Edweard Muybridge - "Freeze frame", pioneer in stop motion photography

Nude descending a staircase, Marcel Duchamp 1912, a scandal when first shown in the Armory show. The object at each moment is at a fixed position (according to Zeno at rest) how can it then move?
The Paradoxa of Zeno of Elea are an example of ancient Greek abstract reasoning that is even in contradiction to observation. How can it be true that nothing moves when our observation “confirms” Heraclitus statement “everything moves and changes”?
Sunday, September 10, 2006
NON - EUCLIDEAN GEOMETRIES
The term non-Euclidean geometry describes hyperbolic, elliptic and absolute geometry, which are contrasted with Euclidean geometry. The essential difference between Euclidean and non-Euclidean geometry is the nature of parallel lines. In Euclidean geometry, if we start with a line l and a point A, which is not on l, then we can only draw one line through A that is parallel to l. In hyperbolic geometry, by contrast, there are infinitely many lines through A parallel to l, and in elliptic geometry, parallel lines do not exist.
In 1829, the Russian Nikolai Ivanovich Lobachevsky published a treatise of hyperbolic geometry. For this reason, hyperbolic geometry is sometimes called Lobachevskian geometry. He was the first to unabashedly claim that Euclidean geometry was not the only geometry, nor the only conceivable geometric structure for the universe. Lobachevsky termed Euclidean geometry, "ordinary geometry," and this new hyperbolic geometry, "imaginary geometry." However, the possibility still remained that the axioms for hyperbolic geometry were logically inconsistent.
Euclidean geometry is modelled by our notion of a "flat plane." The simplest model for elliptic geometry is a sphere, where lines are "great circles" (such as the equator or the meridians on a globe), and points opposite each other are identified (considered to be the same).
Many of the drawings of M. C. Escher embody concepts of non-Euclidean geometry, as expressed in the Poincarémodel of Lobaczewski's plane to Escher's "Circle Limit"



These woodcuts elaborate on illustrations that one can find in various monographs about non-Euclidean geometry.
A casual inspection of Escher's Circle Limit woodcuts suggests a relationship to plane symmetric patterns. Like the latter, a finite motif undergoes an infinite repetition which displays at least combinatorial regularity. Nevertheless, one finds few reflections, glide reflections an gyrations, at least in the Euclidean sense.
It turns out that non-Euclidean geometry requires us to measure distance in a different way. One may compare Poincare''s model, the hyperbolic plane, to a map of the earth. In a typical Mercator projection one finds small distances stretched profoundly near the poles (indeed such maps must omit the poles lest they stretch infinitely up and down). In Poincare''s model one has just the opposite: large hyperbolic distances appear compressed as one travels toward the boundary.
The richness of Poincare''s geometry, the hyperbolic plane, arguably exceeds Euclidean geometry itself. The theory of symmetric patterns gives one indication of this. While symmetric patterns on the Euclidean plane all possess one of 17 symmetry times, symmetric patterns on the hyperbolic plane show inexhaustable variety. Escher's Circle Limit woodcuts show just 4 examples.
The term non-Euclidean geometry describes hyperbolic, elliptic and absolute geometry, which are contrasted with Euclidean geometry. The essential difference between Euclidean and non-Euclidean geometry is the nature of parallel lines. In Euclidean geometry, if we start with a line l and a point A, which is not on l, then we can only draw one line through A that is parallel to l. In hyperbolic geometry, by contrast, there are infinitely many lines through A parallel to l, and in elliptic geometry, parallel lines do not exist.
In 1829, the Russian Nikolai Ivanovich Lobachevsky published a treatise of hyperbolic geometry. For this reason, hyperbolic geometry is sometimes called Lobachevskian geometry. He was the first to unabashedly claim that Euclidean geometry was not the only geometry, nor the only conceivable geometric structure for the universe. Lobachevsky termed Euclidean geometry, "ordinary geometry," and this new hyperbolic geometry, "imaginary geometry." However, the possibility still remained that the axioms for hyperbolic geometry were logically inconsistent.
Euclidean geometry is modelled by our notion of a "flat plane." The simplest model for elliptic geometry is a sphere, where lines are "great circles" (such as the equator or the meridians on a globe), and points opposite each other are identified (considered to be the same).
Many of the drawings of M. C. Escher embody concepts of non-Euclidean geometry, as expressed in the Poincarémodel of Lobaczewski's plane to Escher's "Circle Limit"



These woodcuts elaborate on illustrations that one can find in various monographs about non-Euclidean geometry.
A casual inspection of Escher's Circle Limit woodcuts suggests a relationship to plane symmetric patterns. Like the latter, a finite motif undergoes an infinite repetition which displays at least combinatorial regularity. Nevertheless, one finds few reflections, glide reflections an gyrations, at least in the Euclidean sense.
It turns out that non-Euclidean geometry requires us to measure distance in a different way. One may compare Poincare''s model, the hyperbolic plane, to a map of the earth. In a typical Mercator projection one finds small distances stretched profoundly near the poles (indeed such maps must omit the poles lest they stretch infinitely up and down). In Poincare''s model one has just the opposite: large hyperbolic distances appear compressed as one travels toward the boundary.
The richness of Poincare''s geometry, the hyperbolic plane, arguably exceeds Euclidean geometry itself. The theory of symmetric patterns gives one indication of this. While symmetric patterns on the Euclidean plane all possess one of 17 symmetry times, symmetric patterns on the hyperbolic plane show inexhaustable variety. Escher's Circle Limit woodcuts show just 4 examples.
Synesthetics*
To be able to create artworks which appeal to more than one sense modality artists have to develop creative concepts and skills in which the relation between image and sound -and possible other sense impressions-, are connected in esthetically meaningful ways. During the 20th century many avant-garde artists were fascinated by "creative synesthesia", a state of mind focusing on creating relationships between different artistic media.
The emergence of multimedia technology during the last decades together with the enduring wish of artists to create new forms of "total" art, ask for a practical and theoretical understanding of creative synesthesia and synesthetics.
Dates: September 25, 26, 28, October 2, 3, 5
To be able to create artworks which appeal to more than one sense modality artists have to develop creative concepts and skills in which the relation between image and sound -and possible other sense impressions-, are connected in esthetically meaningful ways. During the 20th century many avant-garde artists were fascinated by "creative synesthesia", a state of mind focusing on creating relationships between different artistic media.
The emergence of multimedia technology during the last decades together with the enduring wish of artists to create new forms of "total" art, ask for a practical and theoretical understanding of creative synesthesia and synesthetics.
Dates: September 25, 26, 28, October 2, 3, 5
